Système de filtre passe bas analogique est modélisé par équa diff :
========================================================

Chaîne d’information :

Grandeur physique -> Capteur -> Conditionnement -> Filtre anti-repliement -> Échantillonnage (Te) -> Filtre numérique -> Décision

1er Ordre:  tau*ds(t)/dt + s(t) = e(t)

le système physique évolue en continu,
!f_max = fréquence max bruit parasite dans le signal analogique

système numérique n’observe le système qu’à des instants discrets.
Te = période d’échantillonnage, temps entre deux acquisitions successives,

Le choix de la période d’échantillonnage doit vérifier :
Te << tau garantit que la discrétisation capture correctement la dynamique du système (on observe le système beaucoup plus vite qu’il n’évolue) et que l’approximation de la dérivée (Euler) reste valide.

Règle empirique :
Te ≤ tau/10
Compromis entre fidélité dynamique et coût de calcul

Théorème de Shannon–Nyquist:
fe = 1/Te > 2*f_max
pas d’aliasing → signal discret exploitable
FAR en amont de l’ADC
conditionne l’efficacité du filtrage numérique aval.
garantit l’absence de repliement spectral ;
Capteur → Filtre anti-repliement → Échantillonnage

Discrétisation d’Euler (implicite) voir Euler avant en bas:
ds/dt ≈ (s[k] – s[k-1]) / Te
la fonction s(t) varie peu sur Te.
fe = 1/Te >> f_c
f_c : fréquence caractéristique du système
f_c ≈ 1/(2*pi*tau)
vitesse à laquelle le système peut réellement évoluer.

paramètre reliant dynamique et échantillonnage:
alpha = Te/(tau + Te)

équation récurrence du filtre numérique :
equa diff + Euler donne:
s[k] = (1 – alpha)*s[k-1] + alpha*e[k]

fonction de transfert dans le domaine Z:
S(z)= (1 – alpha)*z^-1*S(z) + alpha*E[z]
H(z) = S(z)/E(z)=alpha/(1 – (1 – alpha)*z^-1)

condition de stabilité du filtre.:
|z_p| < 1
pôle (dénominateur nul) : z_p = 1 – alpha
si se rapproche trop de 0 ou de 1
filtrage devient soit trop lent, soit inefficace

compromis bruit / rapidité:
alpha petit: (1 – alpha) proche de 1
Moins de bruit en sortie: la sortie dépend surtout de s[k-1],
la nouvelle mesure e[k] est peu prise en compte
les variations rapides sont fortement atténuée
Mais réponse lente: le filtre “réagit lentement” aux changements
montée est progressive, retard plus important
alpha petit → filtrage fort → peu de bruit → réponse lente
tau grand → alpha petit → système lent mais bien filtré
tau petit → alpha grand → système rapide mais bruité

Conclusion : Le paramètre alpha règle le compromis entre atténuation du bruit et rapidité de la réponse : plus alpha est petit, plus le filtrage est fort mais la réponse est lente, et inversement.

Exemple : On mesure une température avec un capteur
================
Chaîne d’info :
Grandeur physique → Capteur → Conditionnement → Filtre anti-repliement → CAN (Te) → Filtre numérique → Décision

On veut réaliser un filtre passe-bas numérique 1er ordre correspondant au modèle analogique :  constante de temps visée : tau = 2,0 s
période d’échantillonnage : Te = 0,20 donc fe = 1/Te
on applique une entrée échelon : x[k] = 1 pour k ≥ 0, avec y[-1] = 0
on a un bruit HF à 12 Hz sur le capteur (sinusoïde parasite)

1) échantillonnage Te << tau : 0,20/2,0 = 0,10
Te = tau/10 → condition Te << tau acceptable (règle pratique)

2) Shannon : fe > 2*f_max, bruit est à f_n = 12 Hz
il faut fe > 24 Hz mais fe=1/0.2=5 aliasing certain!!
donc il faut un FAR avant le CAN ou augmenter fe

3) équation de récurrence:
y[k] = (tau/(tau + Te))*y[k-1] + (Te/(tau + Te))*x[k]
alpha = Te/(tau + Te) = 0,20/(2,0 + 0,20) = 0,20/2,20 = 0,0909
1 – alpha = 0,9091

4) fct transfert en Z
H(z) = alpha/(1 – (1 – alpha)*z^-1) = 0,0909/(1 – 0,9091*z^-1)
Pôle : z_p = a = 0,9091
Stabilité : |z_p| < 1 → |0,9091| < 1 → stable
Le pôle du filtre est à l’intérieur du cercle unité,
donc le filtre est stable.

5) réponse échelon:
alpha ≈ 0,09 (petit) : filtrage fort
(bonne atténuation des variations rapides → bruit réduit)
mais réponse lente (sortie “traîne” sur un échelon :
calculatrice pour itérer l’équation aux différences
comme le ferait le système numérique:
TI nspire CAS Scratchpad -> Graph
menu graph entry
u1(n) =  0.9091*u1(n-1) + 0.0909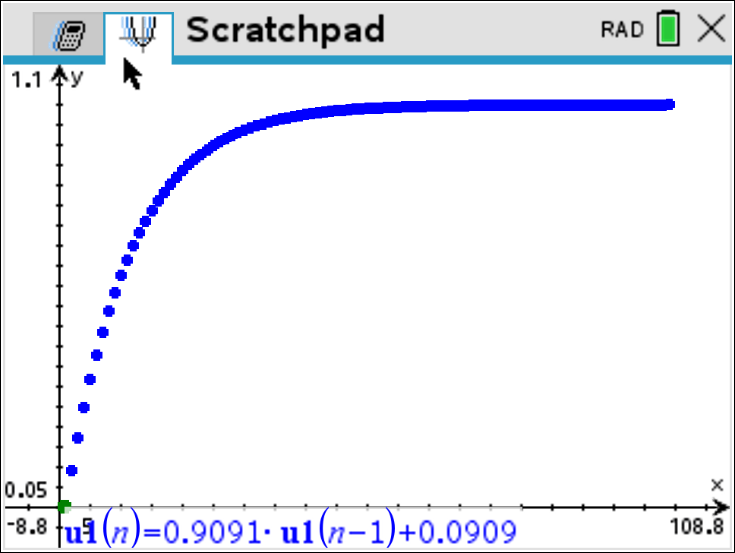
Valeurs initiales := 0
zoom fit
table split screen table 
s(0), s(1), s(2), s(3) affichés

ligne de fonction : s(n)
une montée exponentielle discrète
asymptote vers 1 (échelon)
pente faible → filtrage fort
convergence lente → retard (convergence pour + de 100…)

6) interpréter les résultats :
réponse monotone
pas d’oscillation → pôle réel positif
convergence lente → alpha petit
filtrage efficace du bruit

La réponse indicielle montre une convergence lente et monotone, caractéristique d’un filtre du premier ordre à alpha faible, offrant un bon rejet du bruit au prix d’un retard plus important.

avec alpha fort :
==============
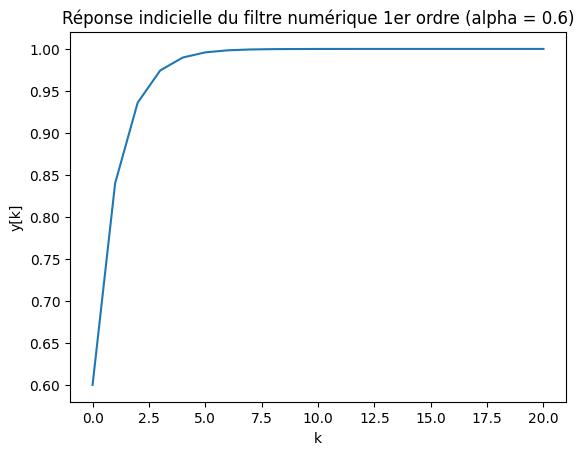
toujours monotone (pas d’oscillation)
montée très rapide:
pente initiale très forte, faible retard
convergence en quelques échantillons
la valeur finale est atteinte quasi immédiatement
La réponse est rapide car le pôle est éloigné de 1
Bruit :
la sortie suit presque directement l’entrée
les variations rapides passent plus facilement

En pratique, Te est souvent imposé par la tâche d’acquisition et la charge CPU. Je choisis tau en fonction de la dynamique utile à conserver, puis j’en déduis alpha = Te/(tau + Te), ce qui fixe le compromis bruit/rapidité. Il faut respecter  Te ≤ tau/10 , fe = 1/Te > 2*f_max
alpha suit automatiquement : alpha = Te/(tau + Te).

Entrée bruitée: on voit avec un alpha faible, les variations rapides sont atténuées, ce qui 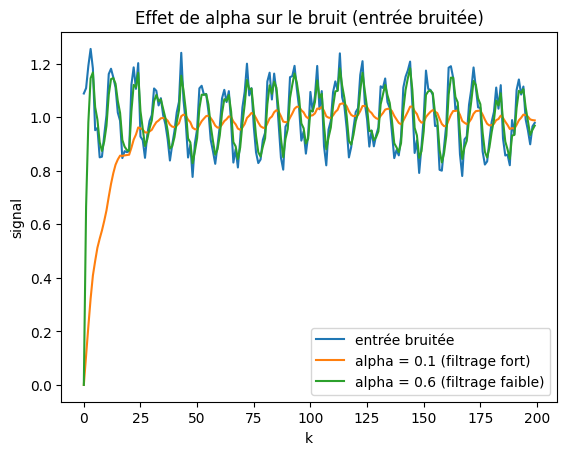améliore le rejet du bruit au prix d’un retard.

Pour voir le bruit, il faut :

• une entrée bruitée, par exemple :

ou :

Alors :

• avec alpha petit → sortie lissée

• avec alpha grand → sortie agitée

👉 C’est là que la différence apparaît.

point de clarification : EULER avant et EULER implicite

Validation filtre numérique “équivalent” à un filtre analogique

Euler implicite: S[n] = (τ / (τ + Tₑ)) · S[n−1] + (Tₑ / (τ + Tₑ)) · e[n]

S[n] dépend linéairement de la valeur précédente S[n−1] et de l’entrée courante e[n], avec un coefficient de pondération lié à τ et Tₑ

Cette relation récursive traduit un filtre numérique du premier ordre, équivalent à un filtre RC analogique, dont la dynamique dépend du rapport entre la période d’échantillonnage et la constante de temps du système.

L’équivalence analogique–numérique est jugée satisfaisante si la valeur absolue de S[n] divisée par s(n·Te), diminuée de 1, reste inférieure à 1 %.
Erreur relative numérique vs analogique  = abs( S[n] / s(n*Te) – 1 )

err_rel(n) = abs( S[n] / s(n*Te) – 1 )

exemple (suite):
on utilise la sortie explicite numérique : S[n]= 1 – (0.9091)^n
et la sortie temporelle: s(n*Te) = 1 – exp(-0.1*n)

err_rel(n) = abs( (1 – 0.9091^n) / (1 – exp(-0.1*n)) – 1 )

!! err_rel(1)  ≈ 4.5 % au premier échantillon

Le critère d’équivalence à 1 % n’est donc pas respecté. L’approximation numérique reste qualitativement correcte mais insuffisante pour une équivalence fine.

Après un certain temps transitoire (acceptable si cahier des charges dit : on s’intéresse à la précision après stabilisation”, “on néglige les premières secondes”.), le filtre numérique devient suffisamment proche du filtre analogique. Le filtre numérique devient satisfaisant pour le suivi lent / en régime, mais pas pour reproduire fidèlement le début du transitoire.

solutions alternatives:

• diminuer TeT_eTe​,

• ou choisir une discrétisation plus fidèle (ZOH exact, bilinéaire…)

• ZOH exact → erreur relative nulle aux instants d’échantillonnage (par construction)

 

Le filtre numérique obtenu par discrétisation Euler constitue donc une approximation satisfaisante du filtre RC analogique pour l’étude temporelle considérée.

Méthode ZOH (équivalence exacte by design)

La discrétisation exacte par maintien d’ordre zéro correspond au comportement réel d’un système commandé par une grandeur échantillonnée maintenue constante entre deux instants. Elle permet d’obtenir un modèle discret fidèle aux instants d’échantillonnage, contrairement aux méthodes d’Euler qui restent des approximations.

Euler avant / arrière → approximation
Bilinéaire  → plutôt culture automatique / fréquentielle
ZOH exact  → équivalence temporelle exacte aux instants d’échantillonnage
S[n] = exp(-Te/tau) * S[n-1] + (1 – exp(-Te/tau)) * e(n*Te)
utiliser alpha = exp(-Te/tau)