1er ordre impact rétroaction (BO->BF): erreur et HBF

Impact rétroaction (BO->BF) pour 1er ordre

1er ordre boucle ouverte BO :

  • Entrée du procédé : e(t)
  • Sortie : s(t)
  • Fonction de transfert BO :
    H_0(p) = S(p)/E(p) = K_0 / (1 + tau_0*p)
  • en temporel : s(t) = E0 * K_f * (1 – exp(-t/tau_f))

K_0 : gain statique du procédé (BO)
K_0 = s(∞)/e(∞)

BF: Évolution du gain et de la constante de temps

H_f(p) = S(p)/E*(p) = H_0(p) / (1 + H_0(p))
H_f(p) = (K_0/(1+tau_0*p)) / (1 + K_0/(1+tau_0*p))
H_f(p) = K_0 / (tau_0*p + 1 + K_0)
H_f(p) = K_f / (1 + tau_f*p) avec
pôle : p_f = -1/tau_f = -(1+K_0)/tau_0)
tau_f = tau_0/(1+K_0)
K_f = K_0/(1+K_0) même résultat pour 2nd ordre!
et ksi_f= ksi_0/(sqrt(1+K_0)) < ksi_0
w0_f=w0 * sqrt(1+K_0) > w0
2ème ordre: ksi diminue et w0 augmente,
attention aux oscillations et instabilité!!

Réponse échelon -> Erreur statique eps_inf  (erreur en régime permanent) :

  • eps_inf = e*(∞) - s(∞)
  • eps(t) = e*(t) – s(t) écart résiduel entre la consigne e* et la sortie s quand le régime transitoire est terminé.
  • BO Laplace definition de l’erreur :S(p) = H_0(p) * EPS(p)
  • avec Rétroactionle comparateur (+//-) donne : EPS(p)=E*(p)-S(p)
  •  la sortie dépend  de l’erreur qui dépend elle même de la sortie : fctmnt de la boucle
  • ces relations combinées nous donne !! après injection de EPS(p) dans S(p)
  • S(p) = H_0(p) · EPS(p) ⇒ EPS(p) = E*(p) − S(p) ⇒ S(p) / E*(p) = H_0(p) / (1 + H_0(p)) = H_f(p)
    ⇒ EPS(p) / E*(p) = 1 − S(p)/E*(p) = 1 / (1 + H_0(p)) ⇒ EPS(p) = E*(p) / (1 + H_0(p))
  • ➝ EPS(p) / E*(p) = 1 / (1 + H_0(p)) (indique quelle part de la consigne n’est pas suivie)
  • th val finale:  eps_inf = lim_{p->0} p*EPS(p) (hyp:pôles de la BF à partie réelle négative)
  • relations combinées → après transformation :
    ➝EPS(p) = E*(p)/(1 + H_0(p)) quand p -> 0
    en BF et pour une consigne échelon  e*(t)=E0*u(t) : E*(p)=E0/p
  • résultat BF: eps_inf = p*EPS(p) * E0/p = p*E0/p* / (1 + H_0) = E0/(1+K_0)
  • robustesse vis-à-vis des incertitudes paramétriques (qd gain varie..)
  • on avait en BO: eps_inf_BO = E0*(1 – K_0)
    • très sensible avec variation du gain K_0 , linéaire, explose vite,pas robuste
    • !! régler K_0=1 pas vraiment possible car le gain varie (température, vieillissement)

-> Réponse indicielle: l’erreur statique dépend slt du gain statique de boucle ouverte K_0.
La rétroaction ne change pas la nature physique du procédé, elle agit comme un diviseur d’erreur : Plus K_0 est grand, plus l’erreur résiduelle est faible. La constante de temps tau_0 n’intervient pas : elle influence la vitesse de réponse, pas la précision finale.
Compromis classique précision–robustesse : augmenter K_0 améliore la précision statique, mais au prix de contraintes accrues sur la stabilité et la sensibilité au bruit.

La rétroaction ne sert pas d’abord à aller plus vite, mais à être juste malgré les incertitudes.

La rétroaction améliore la précision et la robustesse du système, mais seule l’action intégrale permet d’annuler l’erreur statique.

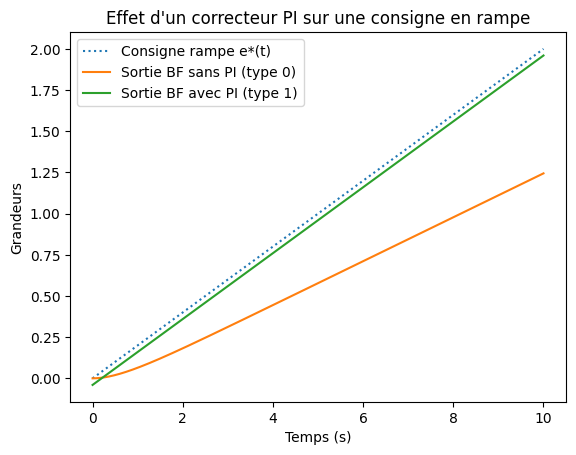
conclusion pour l’écart statique échelon : La rétroaction déplace la valeur finale de la sortie vers la consigne, sans l’atteindre totalement en l’absence d’action intégrale.

Erreur statique – consigne en rampe

  • consigne rampe : e*(t) = a·t·u(t)
  • Laplace : E*(p) = a/p²
  • erreur : eps(t) = e*(t) − s(t)
  • BO Laplace : S(p) = H_0(p) · EPS(p)
  • avec rétroaction (comparateur +/−) : EPS(p) = E*(p) − S(p)
  • relations combinées → après transformation :
  • ➝ EPS(p) = E*(p)/(1 + H_0(p))
  • th val finale :
    eps_inf = lim_{p→0} p·EPS(p) (hyp : BF stable)
  • quand p → 0 : H_0(p) → K_0
  • donc :
    EPS(p) ≃ (a/p²)/(1+K_0)
  • alors :
    eps_inf = lim_{p→0} p·(a/p²)/(1+K_0)
  • ➝ eps_inf → +∞

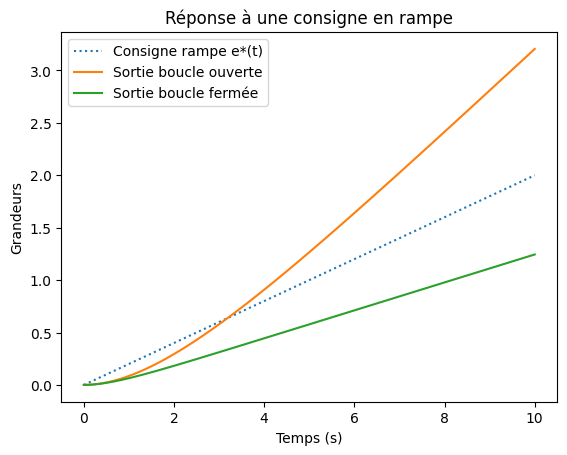
BF_BO_1er_ordre_rampe

  • Pour une consigne en rampe, un système du type 0 (sans intégrateur) est incapable d’assurer un suivi correct en régime permanent. Contrairement au cas de l’échelon, l’erreur ne converge pas vers une valeur finie : elle augmente indéfiniment avec le temps.

  • La rétroaction améliore la dynamique, mais ne suffit pas à compenser une consigne variable.La consigne en rampe augmente linéairement avec le temps.

  • En boucle ouverte, la sortie dépend directement du gain du procédé et s’écarte rapidement de la consigne.

  • En boucle fermée, la sortie suit mieux la rampe, mais avec un retard croissant, traduisant une erreur de poursuite non bornée.

  • L’erreur associée confirme qu’un système sans intégrateur ne peut pas suivre durablement une consigne en rampe.

Dans un asservissement de vitesse, la consigne est très souvent une rampe, correspondant à une phase d’accélération contrôlée (faisant partie d’un profile de vitesse en trapèze) . L’analyse en rampe justifie naturellement l’introduction d’une action intégrale afin de limiter l’erreur de poursuite.

conclusion 1er ordre : Après l’échelon, l’étude d’une consigne en rampe met en évidence les limites fondamentales d’un système sans intégrateur.

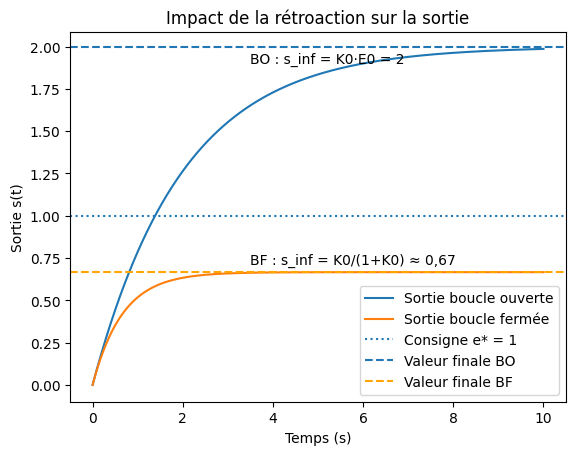
Cas correcteur PI (type 1)

  • correcteur : C(p) = K_p · (1 + 1/(T_i·p)) → intégrateur

  • gain de boucle : H_0(p)·C(p) → pôle en 0 ⇒ type 1

  • consigne rampe e*(t)=a·t :
    eps_inf = a / K_v (erreur finie)

  • ➝ PI : annule la divergence, améliore le suivi de vitesse

L’action intégrale permet de transformer une erreur de poursuite divergente en erreur finie pour une consigne en rampe.

BF_BO_1er_ordre_rampe_PI.